Le module de Young ou le module d'élasticité est une constante propre à chaque matériau qui relie la contrainte (de traction ou de compression) à la déformation du matériau.
Cette constante est employée dans les simulations structurelles pour déterminer la déformation d'une structure sous une charge.
Comment ce module est il déterminé?
Pour déterminer le module de Young d'un matériau, on a recours à un essai de traction ou de compression.
Pour cela, une éprouvette du matériau est placé dans une machine de traction. On mesure alors la force de traction et l'étirement de l’éprouvette. La force exercée est exprimée en une unité de pression, habituellement en GPa (Giga pascal).

Graphique tiré du document sur la théorie des poutres et la résistance des matériaux de www.gecif.net
Le module de Young
Moment quadratique
Simulation réalisée sur le logiciel Solidworks,
Chaque poutre est de la même longueur, possède une section de même aire et une force identique est exercée sur chacune.
La flexion d'une poutre (dans le cas ci-dessus) peut être calculée. Elle est influencée par :
-
La portée de la poutre
-
La force exercée
-
Le module de Young (valeur décrivant les propriétés de chaque matière).
-
Le moment quadratique de la poutre est une valeur définie en fonction de la forme de la poutre, c'est à dire de la répartition de la matière dans la section de la poutre.

Le moment quadratique d'une section est une description de la répartition de la matière dans cette section par rapport à un certain axe. Il est utilisé dans le calcul de la flexion, de compression mais aussi de la traction : il permet de calculer les déformations d'un objet. Cette valeur est exprimée en m4, et peut être calculée mathématiquement. Cependant, la complexité des calculs a entraîné la création d'outils informatiques pour calculer cette valeur.
Certains sites internet permettent de calculer le moment quadratique de différentes formes géométriques basiques tout en détaillant les calculs effectués. Par exemple, grâce à ce site, on observe que le moment quadratique d'une section est plus important lorsque la matière est plus éloignée de l'axe d'étude.
Exemple de l'importance de l'optimisation du moment quadratique :
On observe que certaines poutres fléchissent plus que d'autres. Cela ne peut être causé que par la différence de section qui entraîne un moment quadratique différent. On peut voir que la poutre en I fléchit moins car la matière est éloignée de l'axe de flexion.
La résistance des matériaux

Schéma d'une éprouvette de traction standardisée.

Échantillon de béton en cours d'un test de compression
On peut prendre aussi pour exemple la manière dont la poutre en I fut conçue.
Dans la plupart des cas, la poutre subit une charge provenant de la partie supérieure, ce qui entraîne une flexion de la poutre (dans le cas d'une poutre supportée aux extrémités) mais elle subit aussi une force de compression. Lors de la flexion, le dessus de la poutre est en compression (en rouge) et le dessous est en tension (en bleu). La matière doit donc être répartie majoritairement sur le dessus et sur le dessous comme le montre la coupe ci-contre. Cela permet d'augmenter le moment quadratique et donc d'augmenter la résistance de la poutre.
Il faut d'abord se poser quelques questions :
-
A quelles charges la poutre sera t-elle exposée?
Comment la poutre en I a-t-elle été conçue?
Source : metalaladecoupe.com
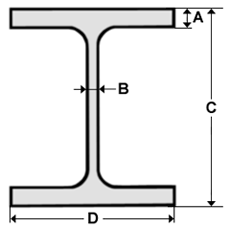
Section d'une poutre en I.

Simulation Solidworks montrant la flexion d'un pont uniquement constitué de poutres en I disposées sur un même plan. On observe que le déplacement des poutres est plus important au centre (les déplacements ont été exagérés par un facteur 10 pour mettre les déplacements importants en valeur).

La résistance des matériaux est un domaine de la mécanique des milieux continus permettant le calcul des contraintes et déformations dans les structures des différents matériaux.